Introduction #
In the early 1600s, a Scottish necromancer took two Greek words, smashed them together, and published in Latin. Ok, maybe he didn't really raise the dead. But I'd imagine that whatever pain would be involved in doing so pales in comparison to the horrors faced by math students when introduced to this Scotsman's word: logarithm.
Historically, logarithms were a revolutionary tool for making computations easier. Yet in my teaching experience, I've found many a student grow frustrated when needing to understand them. And I don't think I'll get much push-back for suggesting that logarithms are one of the more difficult topics for precalculus mathematics courses. My YouTube audience would seem to agree.
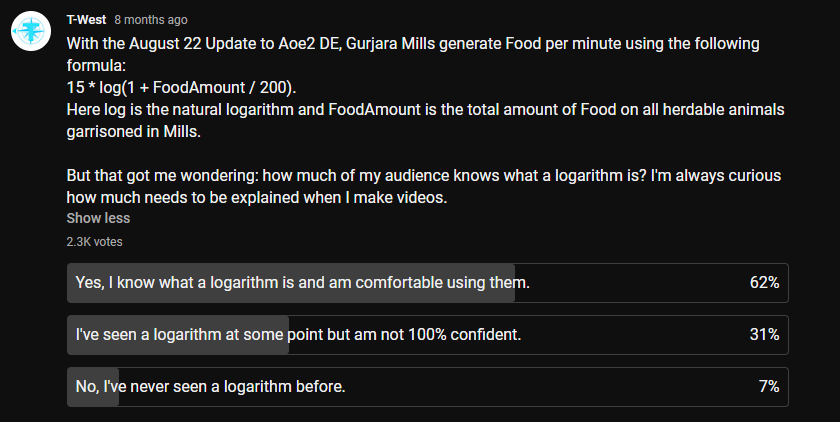
But what exactly makes learning about them so difficult? Maybe it's the need to move beyond the basic operations of addition, subtraction, multiplication, and division. Possibly it's the usage of functions and other mathematical abstractions. Or perhaps it's the intimidating nature of the word itself.
Rather than discuss a topic with which a large percentage of viewers wouldn't be comfortable, I figured this would be a perfect opportunity to put together a math lesson—so welcome to Topics That T-West Thinks Everyone Should Know About Logarithms!
We'll cover the following:
Where the word logarithm comes from and what it means.
The relationship between logarithms and exponents.
How logarithms turn difficult multiplications into easier additions.
The intuition driving various logarithm formulas and properties.
What is
natural
about the natural logarithm and the numberAnd why logarithms result in
fast
algorithms andslow
growth.
Oh, and we'll discuss some Scottish necromancy along the way.
About These Notes #
These notes accompany a YouTube video about logarithms (the link will be posted when the video is uploaded).
Throughout the text, segments of the video corresponding to the relevant topics are embedded.
The notes themselves are availble online at twestaoe
In high school mathematics I'd imagine most students get by without ever reading the textbook. I know I mostly didn't. And to be fair, most of those books probably aren't great reads anyway. But as we advance in our mathematical careers, reading the book becomes a crucial part of the subject. And it can be difficult to learn how to read a math textbook—especially for an algebra or precalculus level where most students don't have any prior experience in doing do.
My hope is that by including videos along with these notes, they become easier to read. And thereby help not just to teach about logarithms, but also to serve as an introduction to reading mathematics. And since a large part of such reading involves solving problems, I've included a variety of exercises throughout the text. They should provide some fun and interesting puzzles to work through.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.